Proof of Normal Distribution Formulas
This density function is a clapper-shaped curve that is approximately µ (see Figure 1). The values of μ and σ2 respectively represent, in a certain sense, the average value and diversity that might occur at X.
The normal distribution
was first introduced by the French mathematician Abraham De Moivre in 1733 and
was used by him to approach opportunities related to the binom probability
distribution if the binom parameter n is large. This finding was later extended
by Laplace and others and is now included in the opportunity theory called the
central limit theorem, which will be discussed in the next article. This
central limit theorem, one of two important findings in probability theory (the
other is a strong law of large numbers), provides a theoretical basis for
empirical observations that are often discovered, namely that many random
phenomena follow, at least approach, a normal distribution of opportunities .
Some examples are height, speed, in any direction from a gas molecule in space,
and errors that occur when measuring a physical quantity.
To prove that f(x) is
indeed a density function of opportunity, we need to understand the derivative
and integrative functions that show that
By substituting y = (x-μ)
/ σ, we get dx = σ dy,
Then,
So, we have to show that
For this purpose, for
example
Then
Now, we will calculate the double integral above through the exchange of
variables to the polar coordinates. For example x = r cos Ɵ, y = r sin Ɵ , dy dx = r dƟ dr. Then,
Because cos2Ɵ + sin2Ɵ = 1 then y2 + x2
y2 + x2 = r2
first, we look for an integral of Ɵ,
Then
For Example u = r2/2 and du = r dr Then
So, I = √2π and prove that
An important fact about
the normal probability distribution is that if X is normally distributed with
parameters μ and σ2, then Y = αX + β is normally distributed with parameters αμ
+ β and α2σ2. This is due to the distribution function Fy,
the cumulative distribution function for the probability distribution Y, given
by,
In this case that equation
(1) is obtained through the variable y = αx + β. However, because
, then from equation 1 it is obtained that the
opportunity density function for Y, namely fr(y),
is
So, Y is
spread normally with parameters αμ + β and (ασ)2.
An
important implication of the above results is that if X spreads normally with
parameters μ and
σ2, then Z = (X – μ)/σ also spreads normally but with parameters 0 and 1. The
probability distribution of Z thus is said to have a standard normal distribution.
Already,
it is customary to symbolize the cumulative distribution function for the
standard normal probability distribution as Φ(x). So,
the values of Φ(x) for
non-negative x are listed in Table 1 below. For negative x values, the value Φ(x) can be obtained from equation (2).
Φ(- x) = 1 - Φ(x) - ∞ < x < ∞ … … … … … (2)
.
Proof of Equation (2) which is a result of the embrace of standard normal density functions, is provided as an exercise. This equation says that if Z is a standard normal probability distribution, then
P{Z ≤ -x} = P{Z > x} - ∞ < x < ∞
Because, Z
= (X – μ)/σ is
a standard normal probability distribution if X is spread normally with
parameters μ and σ2,
the distribution function for X can be written as,
Example 1.
If X is a normal probability distribution with parameters μ = 3 and σ2 = 9, calculate it
P{1 < X < 5}, P{X > 0}, dan P{|X-3| > 6}.
Answer:
Note: Φ(- x) = 1 - Φ(x)
the procedure to get the value of Φ(1/3)= Φ(0.33), Φ(2/3)= Φ(0.66), Φ(1), note
in the following Table 1,
Example 2.
An exam is often considered good (in the
sense of giving a scattered score for those who take it) if the resulting test
score can be approached by a normal density function. (In other words, the
frequency score graph has a clapper shape). Lecturers often use test score
scores to infer normal parameters μ and σ2, and then assign a value of A to those who score greater
than μ + σ, B for those whose values are between μ and μ + σ, C for those whose values
are between μ - σ dam μ, D for those whose
value is between μ - 2σ and μ - σ, and F for those whose value is below μ - 2σ. Because,
Then about 16 percent of the examinees will get an A, 34 percent B, 34 percent C, 14 percent D, and 2 percent F.
Example
3.
An expert
witness in the trial said that the duration (in days) of pregnancy (from
conception to the birth of a baby) spread approximately normally with
parameters μ =
270 and σ2 = 100. The defendant successfully presented evidence that
he was abroad during the period that began 290 days before the baby's birth to
240 days before the baby's birth. If he really is the baby's father, what is
the probability that the mother has a very long or very short pregnancy as
indicated by the defendant's confession?
Solution:
Let X state the length of the pregnancy and assume that the defendant is indeed
the father of the baby in the womb. Then the probability that birth can occur
in that period is?
P{Z ≤ -x} = P{Z > x}
P{-x ≥ Z} = P{x > Z}
The following inequality for Φ(x) contains important theoretical meaning.
To prove the inequality (3.3), examine the truth of the following inequality.
Which implies that
However
So, for x> 0,
And proved Inequality (3).
From the inequality (3) also obtained that
SUBSCRIBE TO OUR NEWSLETTER
























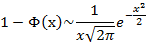

0 Response to "Proof of Normal Distribution Formulas"
Post a Comment