Cumulative Frequency Table (Less Than and Greater Than)

Presentation of data in a frequency distribution is one of the usual first steps in analyzing a data set. Interpreting data can usually be made easier if the data is organized and simplified first. Frequency distribution is a table, where data is grouped in several numerical intervals called classes. The form of this table is very simple because it only presents the number of observations or frequencies in each class interval.

Presentation of the frequency table as stated in the frequency table in the previous article or in the relative frequency table.

Relative Frequency is the ratio between the frequency of each class with the total frequency or the total number of observations. The relative frequency can be in the form of a ratio or a proportion of the total frequency. Relative frequency is very closely related to the distribution of opportunities. Therefore relative frequencies are considered based on observational data. The relative frequency distribution is also called the distribution of empirical opportunities.

In addition to these general and relative frequency distributions, we also know cumulative frequencies. There are two kinds of cumulative frequencies, namely cumulative frequencies which are increasing and decreasing. Increasing cumulative frequencies are also called "frequencies less than", whereas those that decrease increasingly are called "greater than frequencies". As an example we will use the frequency table that has been obtained from the results of calculations in the previous article to find the cumulative value where the table table is as follows:

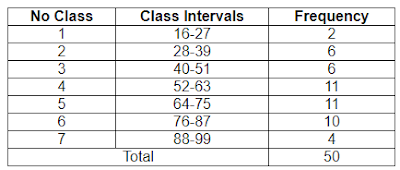
To find the cumulative frequency value "less than" and "greater than" requires 2 new columns, namely the lower and upper limit values. So the table above becomes,

Note:

the way to get the lower bound value is the lowest class interval of a certain class number minus 0.5 => 16 - 0.5 = 15. 5.

While the way to get the upper bound value is the highest class interval from a certain class number plus 0.5 => 27 + 0.5 = 27.5.

From the table above that displays the lower and upper limit values, a cumulative frequency list of less than and more than the following can be made.

Explanation of How to Make Cumulative Frequency Table:

To make the cumulative frequency distribution table less than, we use the upper edge.

1. The first class uses the upper limit of the first class, the second class uses the upper limit of the second class, and so on.
2. The first class has an upper limit of 27.5, so the cumulative frequency of data less than 27.5 is the first class frequency, which is 2.
3. The second class has an upper limit of 39.5, so the cumulative frequency of data less than 39.5 is the frequency of the first class + the frequency of the second class, which is 2 + 6 = 8.
4. The third class has an upper limit of 51.5, so the cumulative frequency of data less than 51.5 is the first class frequency + second class frequency + third class frequency, which is 3 + 6 + 6 = 14.
5. And so on until the seventh class.

To make the cumulative frequency distribution table more than, we use the lower limit.

1. The first class uses the lower limit of the first class, the second class uses the lower limit of the second class, and so on.
2. The first class has a lower limit of 15.5, so the cumulative frequency of data over 15.5 is the frequency of the first class + frequency of the second class + frequency of the third class + ... + frequency of the seventh class = 2 + 6 + 6 + 11 + 11 + 10 + 4 = 50 (Total Frequency).
3. The second class's lower limit is 27.5, so the cumulative frequency of data more than 27.5 is the second class frequency + third class frequency + ... + seventh class frequency = 6 + 6 + 11 + 11 + 10 + 4 = 48 => (Total - First Class Frequency) .
4. And so on until the seventh class.

SUBSCRIBE TO OUR NEWSLETTER

Share this post