Uniform Cumulative Distribution

Cumulative distribution function (fsk) or more concisely the distribution function F for random variable X is defined as

F(b)=P{X≤b}

or all real numbers b, ∞ <b <∞. In words, F (b) states the chance that random variable X takes a value smaller or equal to b. Some properties of f.s.k F are

1.   F is a non-encasing function, meaning that if a <b, then F (a) ≤F (b).

2.   

3.   
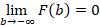
4.   F (b) continuous right, meaning  

In this case lim means the limit for under the condition that every .Character 1 is a result of the fact that if a < b, then the event {X ≤ a} is included in the event {X ≤ b}, so that it cannot have a greater. Properties 2, 3, and 4 are all a result of the continuity of probability. For example, to prove property 2, note that if  , then events converge to event {X <∞} (meaning, if , then lim. Therefore, based on the nature of continuity of opportunity, we get.

Evidence for properties is similar to the above and is provided as an exercise. To prove Nature 4, note that , then . This is a result of the fact that for infinite number of n if and only if {X ≤ b} (so,  ), likewise, for all except for the number n if and only if X≤b (so,) . So  and the continuity character produces,

or

So that is proven Nature 4.

All kinds of opportunity questions about X can be answered based on f.s.k F. For example,

P {a <X ≤ b} = F (b) -F (a) for all a < b .................. equation 1

This is most easily seen if the {X ≤ b} event is pronounced as a combination of events {X ≤ a} and {a < X ≤ b} that set aside each other. In other words.

So that

Which proves equation 1.

If we want to calculate the chance that X is smaller than b, we can also apply the continuity to obtain,

Note that P {X < b} is not always equal to F(b), because F(b) also includes the chance that X is equal to b.

Suppose the function of the random variable X is known as follows,

Calculate (a) P{X<3}, (b) P{X=1}, (c) P{X>1/2}, dan (d) P{2<X≤4}.

SUBSCRIBE TO OUR NEWSLETTER

Share this post