Use Trigonometric Substitution To Solve The Integral Of Square Root
In this article, we will
discuss how to solve integrals that contain the form of square root as follows,
These forms can be changed by substituting functions that contain trigonometry. The basic concept is to change the square root into a simple form of trigonometric function, i.e.
For Example:
For Example:
For Example:
Example 1.
Find the intergral results
from the following equation,
Answer:
To replace sin Ɵ and cos Ɵ, it is necessary to note the trigonometric comparison presented in the following figure,
so that,
Example 2.
Find the intergral results from the following equation,
Answer:
For cot Ɵ, you need to pay attention to the trigonometric comparison presented in the picture on the side.
Example 3.
SUBSCRIBE TO OUR NEWSLETTER

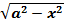
















0 Response to "Use Trigonometric Substitution To Solve The Integral Of Square Root"
Post a Comment