Definition of Vector and Scalar Linear Algebra
In this article we will
discuss the meaning of vectors, especially for vectors on R2 and R3.
Many quantities in physics such as force, speed, acceleration, displacement,
and shift are vectors that can be expressed as directional line segments. The
algebraic view, examines the properties of algebra from a vector space, that
is, the properties of vector addition and scalar vector multiplication. In this
article the properties will be summarized in the discussion on R2
and R3. In addition to physics, vector understanding is also widely
used in other fields outside mathematics such as technology, economics, biology
and so on.
Vector and Vector
Operation
A solution of a system
with m linear equations in n unknown numbers is a tuple-n of real numbers. We
will call a tuple-n real numbers as a vector. If an n-tuple is expressed as a
matrix of 1 x n, we will call it a
row vector. Conversely, if the tuple is expressed by a matrix n x 1, we call it a column vector. For
example the solution of the linear system below,
x1 + x2
= 5
x1 – x2
= 3
then in this section we will explain the presentation and understanding of vectors in geometry and algebra.
Vector Definition of Geometry
Many quantities that we
encounter in science such as: length, mass, volume, and electric charge, can be
expressed by a number.
Such magnitude (and the
number that becomes its size) is called Scalar, There are other quantities,
such as speed, force, torque, and shifts to describe it require not only
numbers, but also directions. Such magnitude is called a Vector. In this
article vectors in space 2 and space 3 will be introduced geometrically, and we
will discuss some of the basic characteristics of this operation.
Vectors can be expressed
geometrically as directed line segments or arrows in space 2 or space 3. The
length of the arrow is the magnitude of the vector while the direction of the
arrow is the direction of the vector. The arrow has a base and a tip (Figure
1). The base of the arrow is called the initial point and the tip of the arrow
is called the terminal point.
We will paint a vector
with bold letters, for example u and
v, because this is rather difficult
to do in writing, you can describe vectors with symbols 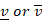
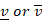
When discussing vectors,
we will declare numbers as scalars. All scalars are real items and will be
expressed by ordinary lowercase letters, for example a, b, c, and k.
If, as in figure 1, the
starting point of the vector v is A
and the terminal point is B, we write it down.
Vectors that have the same
length and direction, such as the vectors in Figure 2, are called equivalents. Because we want a vector
that is determined by its length and direction, the equivalent vectors are
considered equal even though the vectors may be placed in different positions.
Vector operations
For two or more vectors, operations can be carried out as follows,
- Vector addition and subtraction.
- Vector multiplication with scalar.
Provisions in Addition and Reduction of Vector
To obtain the resultant of two vectors u and v, move v without changing the size and direction until the base coincides with the tip u. Then u + v is a vector that connects between the base u and the end v. This method is called the triangular law, which is illustrated in figure 3. Another way of describing u + v is to move v so that the base coincides with the base u. Then u + v is a vector which denies u and which coincides with the diagonal parallelogram whose sides are u and v. This method is called the parallelogram law, which is illustrated in figure 4.
You can prove yourself that this sum is commutative, namely: u + v = v + u.
Vector addition properties
Commutative properties: u +
v = v + u.
Associative properties: (u + v) + w = u + (v + w)
The sum of several vectors does not need to depend on the sequences. Addition can be expanded as shown in figure 6, i.e.,
u = u1
+ u2 + u3 + u4 + u5
This method is called the
polygon method
Vector Multiplication Provisions with Scalar
If u is a vector, then 3u
is a vector that is in the direction of u
but whose length is three times the length u,
the vectors are -2u twice the length
u but in the opposite direction (Figure 7). In general, cu is a scalar multiple of the u
vector, whose length is | c | times the length u, in the direction of u
if c is positive and in the opposite
direction if c is negative.
Specifically, (-1) u (also written as -u) is the same length as u,
but the direction is opposite. This vector is called a negative vector u
because if - u is summed with u, the result is a zero vector (i.e. a
point), this vector is the only vector without a certain direction, called the
zero vector, which is denoted by 0.
This vector is the sum element u + 0 = 0
+ u = u. Finally, the reduction is determined as
u – v = u + (-v)
Example 1.
In figure 8, it is
expressed w with u and v
Solution:
Because u + w = v, then
w = v- u
Example 2.
m = (1-t)u + tv
The evidence we get for m can also be written as
u + t(v - u)
If t changes from - ∞ to + ∞ we get all the vectors leading to the lines shown in the
following figure,
Vector Definition of Algebra
Problems involving vectors can often be simplified by introducing a Cartesian coordinate system. Following this we will limit the discussion of vectors in space-2 and space-3.
Cartesian coordinates in space-2
We begin by taking a
Cartesian coordinate system in the plane. As a representative of u vector, we select an arrow that
starts at the origin (Figure
10). This arrow is determined singly by the coordinates u1 and u2
end points. This means that the vector u
is determined by an ordered pair (u1,
u2) by introducing the
Cartesian coordinate system, which is illustrated in Figure 11. So we assume (u1, u2)
is a vector u. This ordered pair (u1,
u2) is a vector u algebraically.
To form such a coordinate
system, we select an arrow that starts at point 0 as the origin and select two lines that are perpendicular as the
coordinate axis through that origin, which is illustrated in Figure 10 below.
Mark these axes with x and y, then choose a positive direction for each coordinate axis and
also a unit of length to measure distance.
Then we determine the
arrow point by the coordinates u1 and u2.
This means that the vector
u is determined by an ordered pair (u1,
u2).
Vector Operations
Two vectors u = (u1, u2) and v = (v1, v2) are equal (equivalent) if
and only if u1 = v1 and u2 = v2 and apply the following
operations:
Addition and Subtraction
To add u and v, the corresponding components are added, namely:
u + v =
(u1 + v1, u2 + v2)
u + v + w = (u1 + v1 + w1,
u2 + v2 + w2)
u – v =
(u1 – v1, u2 – v2)
Vector multiplication with scalar
To multiply u by scalar k, it is done by multiplying each component with k, namely:
uk = ku = (ku1, ku2)
specifically, u = (-u1,
-u2) dan 0 = 0u = (0,0)
Figure 12 shows that the
above definitions are equivalent to the definitions of Geometry that we
discussed earlier.
Example 3.
- If u = (1, -2) and v = 7, 6) then u + v = (1 + 7, -2 + 6) = (8, 4)
- 4v = 4(7, 6)= (4 (7), 4 (6)) = (28, 24)
Cartesian Coordinate in Space-3
Vectors in space 3 can be
expressed by triple real numbers, by introducing the Cartesian coordinate
system depicted in Figure 13
below,
If, as Figure 13 above
vector v in room 3 is located so
that the starting point is at the origin of the Cartesian coordinate system,
the coordinates of the terminal point are called components v and we write them as,
v = (v1, v2, v3)
Vector Operations
Two vectors v = (v1, v2,
v3) and w = (w1, w2,
w3) are equivalent if and
only if v1 = w1, v2 = w2,
and v3
= w3.
To add v = (v1, v2,
v3) and w = (w1, w2,
w3), we add the
appropriate components, namely
v + w =
(v1 + w1, v2 + w2,
v3 + w3)
to multiply vector v with scalar k, we multiply each component with k, i.e.
vk = kv =
(k v1, k v2, k v3)
Example 4.
If v = (1, -3, 2) and w = (4, 2, 1) then
v + w = (1 +
4, -3 + 2, 2 + 1)= (5, -1, 3)
2v = (2(1),
2(-3), 2(2))=(2,-6,4)
v-w=v+(-w) = (1 +
(-4), -3 + (-2), 2 + (-1)) = (-3, -5, 1)
If the vector 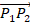 has a starting point at P1 (x1,
y1, z1) and the terminal point in P2(x2,
y2, z2), then:
has a starting point at P1 (x1,
y1, z1) and the terminal point in P2(x2,
y2, z2), then:
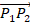 has a starting point at P1 (x1,
y1, z1) and the terminal point in P2(x2,
y2, z2), then:
has a starting point at P1 (x1,
y1, z1) and the terminal point in P2(x2,
y2, z2), then:
That is, the components
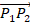 we get by
subtracting the coordinates of the starting point from the coordinates of the
terminal point. This can be seen using Figure 14 below,
we get by
subtracting the coordinates of the starting point from the coordinates of the
terminal point. This can be seen using Figure 14 below,
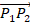 we get by
subtracting the coordinates of the starting point from the coordinates of the
terminal point. This can be seen using Figure 14 below,
we get by
subtracting the coordinates of the starting point from the coordinates of the
terminal point. This can be seen using Figure 14 below,
Example 5.
Solution:
SUBSCRIBE TO OUR NEWSLETTER




















0 Response to "Definition of Vector and Scalar Linear Algebra"
Post a Comment