Definitions of Inverse Matrix and Proof of Inverse Matrix Formulas

In this article, we will discuss the definition of inverse matrix that solve using elementary row operations and apply these operations simultaneously to In to get A^-1.

Often it will not be known in advance whether a matrix can be reversed. If the matrix cannot be reversed, then the matrix is in the form of a reduced line echelon that has at least a zero number row and will appear on the left hand side. So, if the given matrix cannot be reversed, the calculation can be stopped.

In connection with that, the method that will be used to perform the procedure is the Gauss-Jordan elimination method. This method will increase the superiority of its application even though the given matrix cannot be reversed.

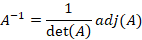
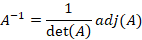
Definition of inverse matrix

A quadratic matrix A has the n expressed as

It is called having an inverse if there is a matrix B, so AB=BA=I_n, then A is said to be invertible. B matrix is called inverse matrix A (invertible), written A^-1, is a quadratic matrix with n.

Example 1.

Calculate the inverse of

Solution:

For Example,

When multiplied it will be obtained:

So that the equation produced is

To get the values of a₁, a₂, a₃, and a₄ then the suitable method is the Gauss-Jordan elimination method which will add the first line to the second row,

First column,

Get a value of a₁,