Estimated Parameters of the decimated Poisson Distribution
The random X variable is said to follow a truncated Poisson distribution with a parameter λ, if it has the following probabilities function:
The expectations of the random X variable that follows the decimated Poisson distribution above are
The expectations of the random X variable that follows the decimated Poisson distribution above are
Suppose X1, X2, ... Xn is a random sample of size n from a decrepit Poisson distribution, then the estimated parameter λ can be obtained by equating the average sample data with its expectations, so that
Where,
Take the average sample data as the initial value of 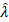 . So
. So 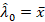 . The iteration at Equation 5 above is stopped until the convergent value of
. The iteration at Equation 5 above is stopped until the convergent value of 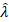 is obtained. One of the convergence rules is:
is obtained. One of the convergence rules is:
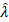 . So
. So 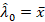 . The iteration at Equation 5 above is stopped until the convergent value of
. The iteration at Equation 5 above is stopped until the convergent value of 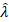 is obtained. One of the convergence rules is:
is obtained. One of the convergence rules is:
The value of 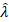 when converging occurs, is the estimated value of the parameter λ. Example 1 below pertains to finding parameter estimated values from a decimated Poisson distribution.
when converging occurs, is the estimated value of the parameter λ. Example 1 below pertains to finding parameter estimated values from a decimated Poisson distribution.
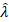 when converging occurs, is the estimated value of the parameter λ. Example 1 below pertains to finding parameter estimated values from a decimated Poisson distribution.
when converging occurs, is the estimated value of the parameter λ. Example 1 below pertains to finding parameter estimated values from a decimated Poisson distribution.Examples of Calculating Estimated Poisson Distribution Parameter Value Values
Suppose that the data we have data that has been formed into a vector where the data is [4 3 3 2 1 1 5 6 4 4 2 2 4 3 3] with a total sample number n = 15. From these data, calculate the estimated Poisson Poisson Distribution Parameters and the Iterations for the value of 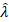 which converges using the calculation manually and using the Matlab Software. Compare the results of both, is it the same?
which converges using the calculation manually and using the Matlab Software. Compare the results of both, is it the same?
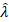 which converges using the calculation manually and using the Matlab Software. Compare the results of both, is it the same?
which converges using the calculation manually and using the Matlab Software. Compare the results of both, is it the same?The manual calculation,
Then is it iterated k = 0 already convergent,
Then is it iterated k = 1 already convergent,
Then is it iterated k = 2 already convergent,
From the results of the manual calculation above the Parameter Estimation Value of the Poisson Convergent Distribution in Vector Value X = 2.9727 at k = 2 which is the 3rd literacy process.
Calculation Using Matlab Software
1. Make the calculation function and save it with the file name examplePois.m
function lambda = examplepois(data)
% calculate the estimated value of the parameter
% from an iterated Poisson distribution
% Using the Newton method
% with the initial value of the sample data
rata=mean(data);
lambda(1)=rata;
sel=1;
k=0;
while sel>=0.00001
k=k+1;
a=(lambda(k)-rata*(1-exp(-lambda(k))));
b=(1-rata*exp(-lambda(k)));
lambda(k+1)=lambda(k)-a/b;
sel=abs(lambda(k+1)-lambda(k));
end
k=k-1 %to get the value of k
literasi=k+1 %to get literacy
end
2. Run in the Command Window Matlab.
If comparing the results between manual calculations using Matlab, the results are not much different. The difference caused usually occurs because of the influence of the number of uses of decimal digits when performing calculations.
SUBSCRIBE TO OUR NEWSLETTER























Thanks sir, iam understand about in article, you make me understand more about it :)
ReplyDeleteNice info
ReplyDeleteThanks for information because make me to be smart
ReplyDelete